Rule #3: Every decision involves trade-offs
One of the universal rules of decision-making is that every decision involves trade-offs. By definition, when making a decision, you are trading off one option for another. But other, less obvious trade-offs are also lurking beneath the surface.
For example, whatever you choose now will send you down a path that will shape your future decisions, a mental model known as path dependence. That is, your future path is both influenced and limited by your past decisions. If you enroll your child in a language immersion school, you significantly increase the chances that they will move to an area of the world where that language is spoken, decades from now. Maybe you're OK with that possible path, but you should at least be aware of it.
In a real sense, you aren’t just trading the immediate outcomes of one option for another, but one future path for another. From that perspective, you can consider path-related dimensions, such as how the various options vary in terms of future optionality or reversibility. It’s not that more optionality or reversibility is always better, as often they come at a cost, but just that these less-obvious trade-offs should be considered.
A related, less-obvious trade-off involves opportunity cost. If you pick from the options in front of you, what other opportunities are you forgoing? By explicitly asking this question, more options might reveal themselves. And, you should also always ask specifically what opportunities you are forgoing by deliberating on the decision. Sometimes waiting too long means you miss out on the best option; other times, putting off the decision means more options will emerge. Again, one side isn’t always better, since every situation is different. But the opportunity costs, including from waiting, should be explored.
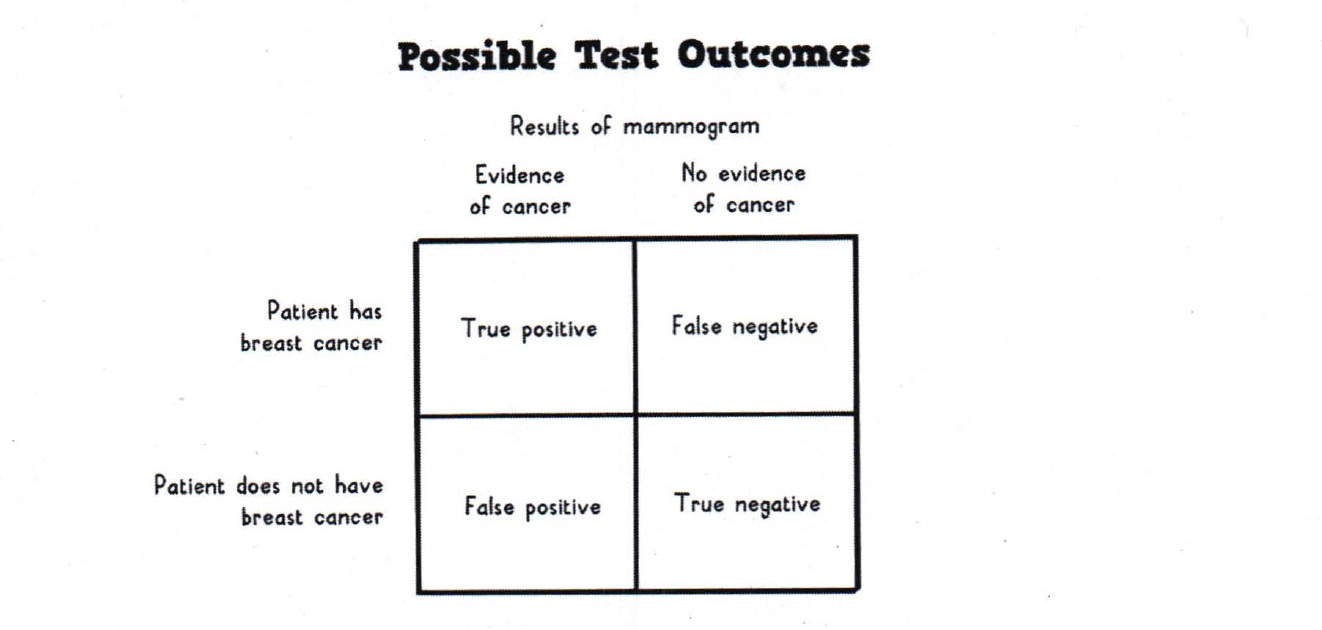
Another common but less-obvious trade-off concerns the different types of errors you can make in a decision. From our book Super Thinking:
[C]onsider a mammogram, a medical test used in the diagnosis of breast cancer. You might think a test like this has two possible results: positive or negative. But really a mammogram has four possible outcomes…the two possible outcomes you immediately think of are when the test is right, the true positive and the true negative; the other two outcomes occur when the test is wrong, the false positive and the false negative.
These error models occur well beyond statistics, in any system where judgments are made. Your email spam filter is a good example. Recently our spam filters flagged an email with photos of our new niece as spam (false positive). And actual spam messages still occasionally make it through our spam filters (false negatives). Because making each type of error has consequences, systems need to be designed with these consequences in mind.
That is, you have to make decisions on the trade-off between the different types of error, recognizing that some errors are inevitable. For instance, the U.S. legal system is supposed to require proof beyond a reasonable doubt for criminal convictions. This is a conscious trade-off favoring false negatives (letting criminals go free) over false positives (wrongly convicting people of crimes).
To uncover other less obvious trade-offs, you can brainstorm and explicitly list out (for example, in a spreadsheet) the more subtle dimensions on which options differ. Think of a comparison shopping page that compares numerous features and benefits. The obvious ones — such as cost — may immediately come to mind, but others may take time to surface, like how choosing one option might impact your personal quality of life in the future.
The point is not to overthink decisions, but to be conscious about inherent trade-offs, especially the less obvious yet consequential ones. Just as I think you should take the time to write out assumptions explicitly, I also believe you should do the same for trade-offs.
See other Rules.
The Transporter (2002)


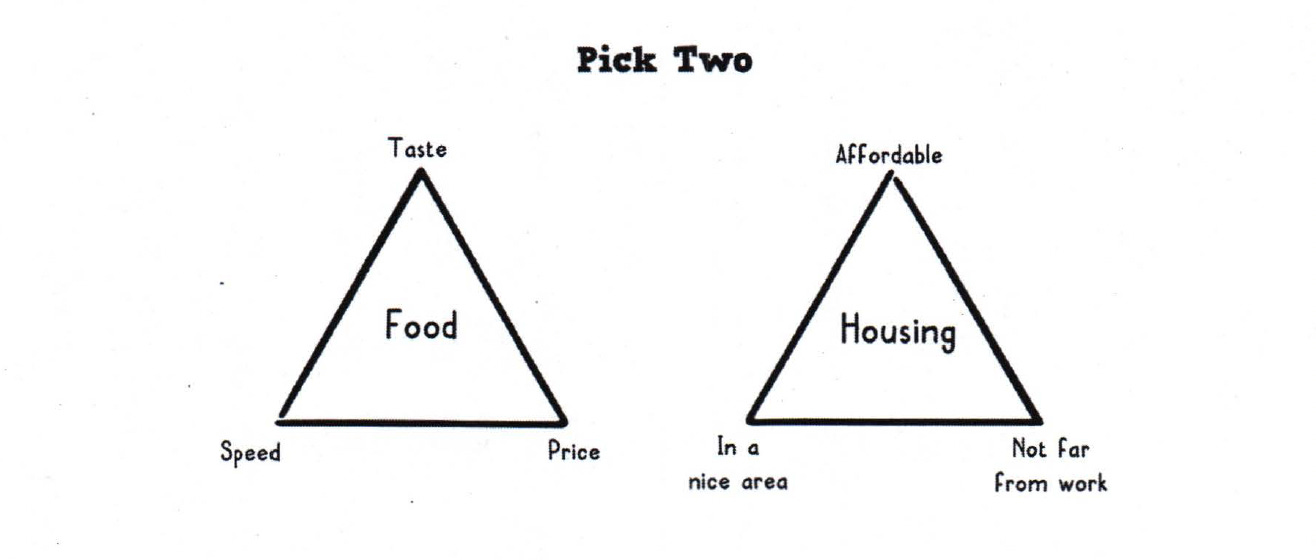
The obvious one you seem to have avoided (maybe deliberately? ;-) is in software engineering. Pick 2: Speed, Quality, Cost. The thing is I have never really thought that is a great example because there may be other factors related to why you can't pick one or the other. For example if you're building a product and want to maintain speed and quality then cost will go up, but that only works to a point before diminishing returns because of the mythical man-month. Then what confounds me is that clever people who are making those decisions ignore Brooke's Law and think they can still push for speed while maintaining quality because they are happy for costs to go up. But the rising costs aren't actually contributing anything to the process. As a result, you end with "pick 1" - speed or quality.
Really enjoyed this - the triangle is great for visualising and articulating trade-offs beyond the binary, and writing out assumptions to make them clear. Love it